
In other circumstances however this is not accepteble. It is rather acceptable to ignore the centroidal term for the flange of an I/H section for example, because d is big and flange thickness (the h in the above formulas) is quite small. Usually in enginnereing cross sections the parallel axis term $Ad^2$ is much bigger than the centroidal term $I_o$. $$ I = 2\left(1666666.7 + 5000000 \right) \,mm^4 $$ The Moment of inertia of circular section is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis is calculated using mioftheareaofsection (pi (Radius of circle 4))/4.To calculate Moment of inertia of circular section, you need Radius of circle (r).With our tool, you need to enter the respective value for Radius of circle and.
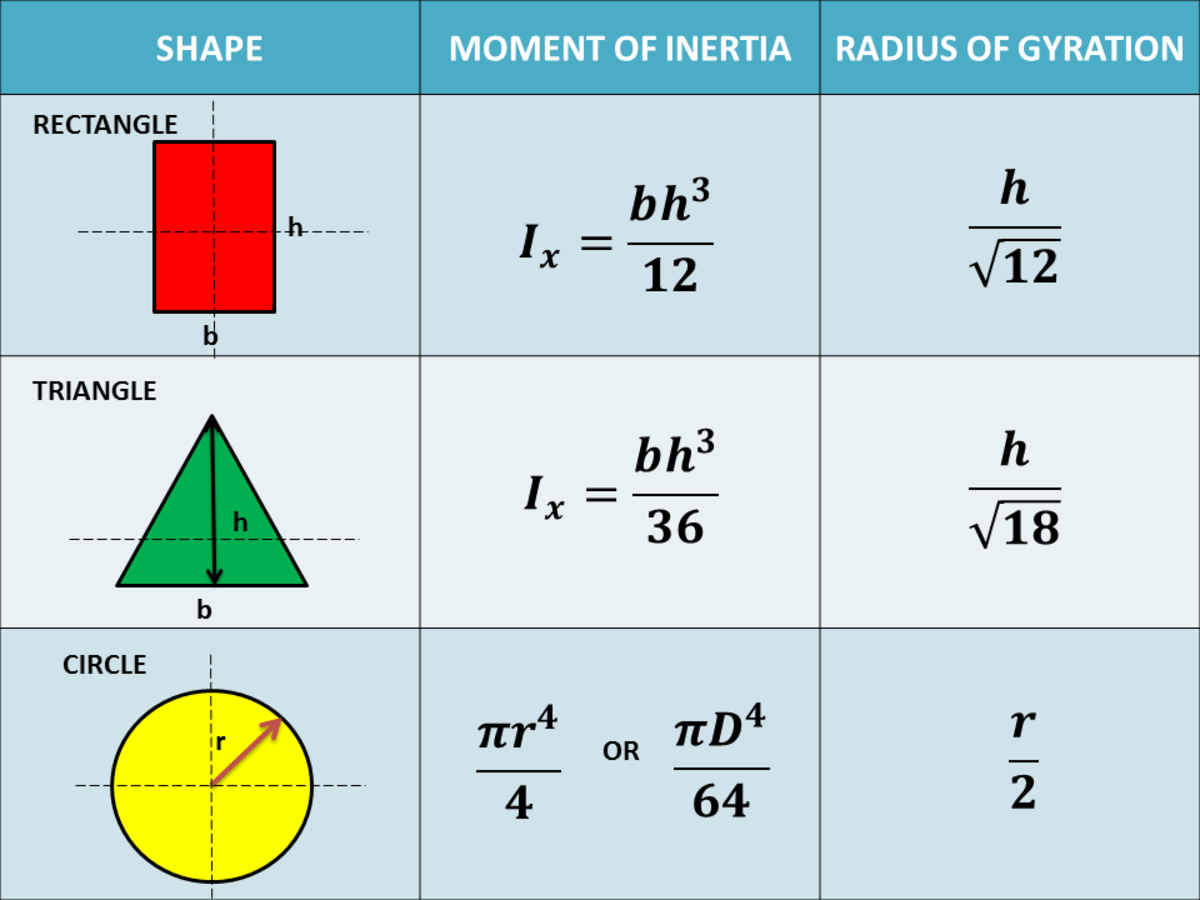
I moment of inertia (in 4) d o outside diameter (in) d i inside diameter (in) Section Modulus. I_x &= \int\limits_ + 20\cdot 100\cdot\left(50\right)^2 \right)\,mm^4$$ The calculator is based on the piping formulas and equations below.
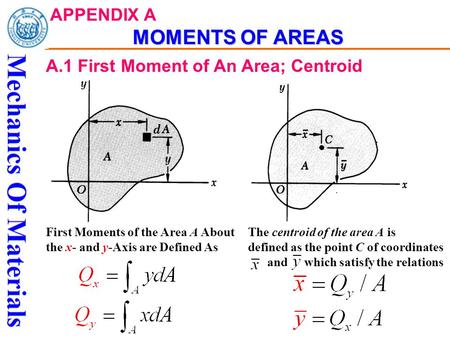
In the case of a rectangular section around its horizontal axis, this can be transformed into Where $\rho$ is the distance from any given point to the axis. The moment of inertia of an object around an axis is equal to
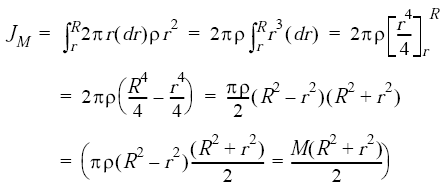
You have misunderstood the parallel axis theorem.


 0 kommentar(er)
0 kommentar(er)
